Containers scheduling#
Description: Scheduling model for harbor operations. It is a problem with dependences between containers, which should be dispatch the fastest possible. We are using the MP solver interfaces to model a complex system using techniques from Constraint Programming, such as indicator constraints, and logical or and forall operators. After the model is written, a couple instances are presented and Highs/Gurobi MIP solvers are used to tackle the problem.
Tags: amplpy, scheduling, industry, mip, constraint-programming, mp
Notebook author: Marcos Dominguez Velad <marcos@ampl.com>
# Install dependencies
%pip install -q amplpy
# Google Colab & Kaggle integration
from amplpy import AMPL, ampl_notebook
ampl = ampl_notebook(
modules=["highs", "gurobi"], # modules to install
license_uuid="default", # license to use
) # instantiate AMPL object and register magics
Containers scheduling#
The harbor wants to dispath the most containers possible, so they can be shipped soon.
The container scheduling problem is a general scheduling problem where we want to move some containers (tasks) with some cranes (the agents). However, containers are dependent between themselves, as they are grouped in stacks. Then, we can’t dispatch a container until we have dispatched every container above it.
There are work periods / shifts in which machines can work.
Multiple stacks of containers
Different cranes
Model#
Sets and parameters#
Set of containers \(C\), each container is descripted by 2 coordinates: \((i,c)\). \(i\) is the stack of the container, and \(c\) the order inside the stack. Blocks/stacks of containers are independent, but 2 machines can be working on the same stack during a period of time.
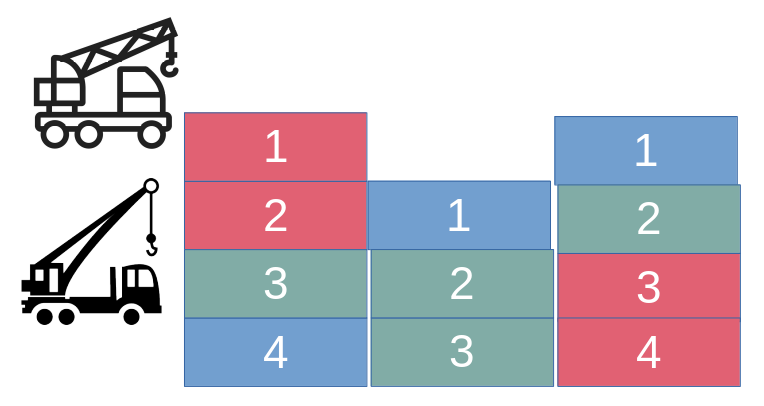
Set of periods of time \(T\). These periods are assume to be equal.
Set of machines \(M\). Each machine has a work capacity to move the containers.
To dispatch a container, we have to work at least the move cost of a container.
Variables#
\(c\_moving_{m,i,c,t}\): binary variable equals 1 if machine \(m\) is working on container \((i,c)\) in period \(t\), 0 otherwise.
\(c\_end_{i,c,t}\): binary variable equals 1 if the container \((i,c)\) is already dispatched in period \(t\), 0 otherwise. If we finish a container in time \(t\), then \(c\_end\) should be 1, although it wasn’t finished at the beginning of the time period.
\(c\_progress_{m,i,c,t}\): continuous \(\geq 0\) variable that saves the amount of work we did on container \((i,c)\) in period \(t\) with machine \(m\).
The rest of the model are constraints that give meaning and bounds to these variables. We are using some Constraint Programming operators to write the model efficiently.
Constraints#
Maximum progress of container \((i,c)\):
\[
\sum \limits_{m \in M, t \in T} c\_progress_{m,i,c,t} \leq move\_cost_{i,c}
\]
in ampl:
subject to progress_limit_container{(i,c) in C}:
sum{m in M, t in T} c_progress[m,i,c,t] <= move_cost[i,c];
Maximum work of machine \(m\) in time \(t\):
\[
\sum \limits_{(i,c) \in C} c\_progress_{m,i,c,t} \leq work\_cap_m
\]
in ampl:
subject to progress_limit{m in M, t in T}:
sum{(i,c) in C} c_progress[m,i,c,t] <= work_cap[m];
Bonds between variables…
Bond between move and progress:
\[
c\_mov_{m,i,c,t} = 1 \iff c\_progress_{m,i,c,t} > 0
\]
in ampl:
subject to active_work{m in M, (i,c) in C, t in T}:
c_moving[m,i,c,t] = 1 <==> c_progress[m,i,c,t] > 0;
(logical constraints are linearize through the MP solver interfaces)
Bond between end a container and progress:
\[
c\_end_{i,c,t} = 1 \iff \sum \limits_{m \in M, \; t' = 1}^{t} c\_progress_{m,i,c,t'} = move\_cost_{i,c}
\]
subject to finish{(i,c) in C, t in T}:
c_end[i,c,t] = 1 <==> sum{m in M, t_ in 1..t} c_progress[m,i,c,t_] >= move_cost[i,c];
Containers logic constraints…
Containers are in a stack:
\[
c\_mov_{m,i,c,t} \leq c\_end_{i,c-1,t}\;, \quad \forall m \in M, (i,c) \in C: \ c \neq 1, \; t \in T
\]
in ampl:
subject to previous_container{m in M, (i,c) in C, t in T: c > 1}:
c_moving[m,i,c,t] <= c_end[i,c-1,t];
A finished container doesn’t move:
\[
c\_end_{\, i,c,t} = 1 \implies c\_mov_{m,i,c,t+1} = 0
\]
in ampl:
subject to already_finished{m in M, (i,c) in C, t in T: t <> last(T)}:
c_end[i,c,t] = 1 ==> c_moving[m,i,c,t+1] = 0;
We need to move every container.
\[
c\_end_{\, i,c,last(T)} = 1, \quad \forall (i,c) \in C
\]
in ampl:
subject to finish_all{(i,c) in C}:
c_end[i,c,last(T)] = 1;
\(c_end\) variable is monotonous, so we can write some constraints to strengthen the model so it gets solved faster.
\[
c\_end_{\, i,c,t-1} \leq c\_end_{\, i,c,t}, \quad \forall (i,c) \in C, \ \forall t \in T \setminus \{ 1 \}
\]
\[
c\_end_{\, i,c-1,t} \geq c\_end_{\, i,c,t}, \quad \forall (i,c) \in C: \ c \neq 1 \ \forall t \in T
\]
in ampl:
c_end[i,c,t-1] <= c_end[i,c,t];
c_end[i,c-1,t] >= c_end[i,c,t];
If a machine is moving a block, no other machine can use it.
\[
\sum \limits_{(i',c) \in C: \ i = i'} c\_mov_{i,c,t} \geq 1 \implies \forall_{\substack{(i', c) \in C: \ i != i'}} \ c\_mov_{i',c,t} = 0
\]
in ampl:
subject to only_one_block{m in M, i in B, t in T}:
sum{(i_,c) in C: i == i_} c_moving[m,i,c,t] >= 1 ==> forall{(i_, c) in C: i != i_} c_moving[m,i_,c,t] = 0;
Finish the partially moved containers.
\[
c\_mov_{m,i,c,t-1} = 1 \implies c\_mov_{m,i,c,t} = 1 \lor c\_end_{i,c,t-1} = 1
\]
in ampl:
subject to cant_forget_active_containers{m in M, (i,c) in C, t in T: t != last(T)}:
c_moving[m,i,c,t] = 1 ==> c_moving[m,i,c,t+1] = 1 or c_end[i,c,t] = 1;
A container is only dispatched by 1 machine:
\[
\sum \limits_{m \in M} c\_mov_{m,i,c,t} \leq 1
\]
in ampl:
subject to one_mach_per_container{(i,c) in C, t in T}:
sum{m in M} c_moving[m,i,c,t] <= 1;
Objective#
We have no objective in this problem, but if we can add some of them to get “better” feasible solutions. For example, giving some penalties to delayed blocks or unused capacity of the machines.
\[
\min \quad delay\_penalty + unused\_cap\_penalty
\]
where
\[
delay\_penalty = \sum \limits_{(i,c) \in C, \; t \in T} (1-c\_end_{\, i,c,t })
\]
\[
unused\_cap\_penalty = \sum \limits_{m \in M, \; (i,c) \in C, \; t \in T} \frac{t}{|T|} \cdot \frac{c\_progress_{m,i,c,t}}{total\_move}
\]
in ampl:
var delay_penalty = sum{(i,c) in C, t in T} (1-c_end[i,c,t]);
var unused_cap_penalty = sum{m in M, (i,c) in C, t in T} t/card(T)*c_progress[m,i,c,t]/total_move;
minimize penalty: unused_cap_penalty + delay_penalty;
With this formulation, we get a neat model easy to read despite of being a complex system.
We are using many logical constraints such as indicator constraints, logical operators (or and forall), but we can still use a MIP solver such as Highs or Gurobi to solve the problem due to the driver’s reformulation.
%%ampl_eval
reset;
# Blocks
set B;
# Time periods
set T ordered;
# Containers
set C dimen 2; # (block, container)
# Machines
set M;
# Cost per container
param move_cost{C};
param total_move := sum{(i,c) in C} move_cost[i,c];
# Work capacity of the crane
param work_cap {M};
# Vars #
# Container in progress, container is finished, container progress units
var c_moving{M,C,T} binary;
var c_end{C,T} binary;
var c_progress{m in M,C,T} >= 0 <= work_cap[m];
# Constraints #
## Container completion
# Cant progress more than available in the container
subject to progress_limit_container{(i,c) in C}:
sum{m in M, t in T} c_progress[m,i,c,t] <= move_cost[i,c];
# Cant progress more than available by the machine
subject to progress_limit{m in M, t in T}:
sum{(i,c) in C} c_progress[m,i,c,t] <= work_cap[m];
## Containers logic
# Active iff in progress:
subject to active_work{m in M, (i,c) in C, t in T}:
c_moving[m,i,c,t] = 1 <==> c_progress[m,i,c,t] > 0;
# c_moving[m,i,c,t] = 1 <==> c_progress[m,i,c,t] >= 1e-9;
# if completely moved then finish container.
subject to finish{(i,c) in C, t in T}:
c_end[i,c,t] = 1 <==> sum{m in M, t_ in 1..t} c_progress[m,i,c,t_] >= move_cost[i,c];
# A container is not active unless previous has finished:
subject to previous_container{m in M, (i,c) in C, t in T: c > 1}:
c_moving[m,i,c,t] <= c_end[i,c-1,t];
# A container is not active if it already finished:
subject to already_finished{m in M, (i,c) in C, t in T: t <> last(T)}:
c_end[i,c,t] = 1 ==> c_moving[m,i,c,t+1] = 0;
subject to finish_all{(i,c) in C}:
c_end[i,c,last(T)] = 1;
# Finished container can't go unfinished
subject to remain_finished{(i,c) in C, t in T: t <> last(T)}:
c_end[i,c,t] <= c_end[i,c,t+1];
# Cant go to other blocks
subject to only_one_block{m in M, i in B, t in T}:
sum{(i_,c) in C: i == i_} c_moving[m,i,c,t] >= 1 ==> forall{(i_, c) in C: i != i_} c_moving[m,i_,c,t] = 0;
# Cant forget containers
subject to cant_forget_active_containers{m in M, (i,c) in C, t in T: t != last(T)}:
c_moving[m,i,c,t] = 1 ==> c_moving[m,i,c,t+1] = 1 or c_end[i,c,t] = 1;
# One machine per container atmost
subject to one_mach_per_container{(i,c) in C, t in T}:
sum{m in M} c_moving[m,i,c,t] <= 1;
# Objective #
var delay_penalty = sum{(i,c) in C, t in T} (1-c_end[i,c,t]);
#var delay_penalty_scaled = sum{c in C, t in T} (1-c_end[c,t])/card({C,T});
# Scaled!!
var unused_cap_penalty = sum{m in M, (i,c) in C, t in T} t/card(T)*c_progress[m,i,c,t]/total_move;
minimize penalty: unused_cap_penalty + delay_penalty;
Solving a simple instance#
We are using the open source solver highs to solve an instance of the problem:
def container_cost(i, l):
return max(3, (i + l) % 7)
periods = 10
containers = 4
blocks = 2
machines = 2
container_costs = {
(i, l): container_cost(i, l)
for i in range(1, blocks + 1)
for l in range(1, containers + 1)
}
print(container_costs)
work_capacity = {m: 5 for m in range(1, machines + 1)}
ampl.set["T"] = range(1, periods + 1)
ampl.set["B"] = range(1, blocks + 1)
ampl.set["M"] = range(1, machines + 1)
ampl.set["C"] = [(i, l) for i in range(1, blocks + 1) for l in range(1, containers + 1)]
ampl.param["move_cost"] = container_costs
ampl.param["work_cap"] = work_capacity
ampl.solve(solver="highs")
assert ampl.solve_result == "solved", ampl.solve_result
# ampl.display('c_moving')
# ampl.display('c_end')
ampl.display(
"{m in M, (i,c) in C, t in T : c_progress[m,i,c,t] >= 1e-6} c_progress[m,i,c,t]"
)
{(1, 1): 3, (1, 2): 3, (1, 3): 4, (1, 4): 5, (2, 1): 3, (2, 2): 4, (2, 3): 5, (2, 4): 6}
HiGHS 1.8.1: optimal solution; objective 10.21818182
7327 simplex iterations
22 branching nodes
absmipgap=3.55271e-15, relmipgap=0
c_progress[m,i,c,t] :=
1 2 1 1 3
1 2 2 1 2
1 2 2 2 2
1 2 3 2 3
1 2 3 3 2
1 2 4 3 3
1 2 4 4 3
2 1 1 1 3
2 1 2 1 2
2 1 2 2 1
2 1 3 2 4
2 1 4 3 5
;
Solving a more difficult instance#
We are using Gurobi, a powerful commercial solver to solve the instance. Notice that we are using timeout=150s so Gurobi only runs for 150 seconds, which is enough for giving a good solution.
We can check some stats of the solving process through the outlev=1 option.
(If you are using a Community Edition from Google Colab, you can change to the ‘highs’ solver and try to solve the instance)
def container_cost(i, l):
return max(3, (i + l * 17) % 10)
periods = 20
containers = 8
blocks = 4
machines = 3
container_costs = {
(i, l): container_cost(i, l)
for i in range(1, blocks + 1)
for l in range(1, containers + 1)
}
work_capacity = {m: 5 + m for m in range(1, machines + 1)}
ampl.set["T"] = range(1, periods + 1)
ampl.set["B"] = range(1, blocks + 1)
ampl.set["M"] = range(1, machines + 1)
ampl.set["C"] = [(i, l) for i in range(1, blocks + 1) for l in range(1, containers + 1)]
ampl.param["move_cost"] = container_costs
ampl.param["work_cap"] = work_capacity
ampl.solve(solver="gurobi", gurobi_options="outlev=1 timelim=150")
assert ampl.solve_result in ["solved", "limit"], ampl.solve_result
# ampl.display('c_moving')
# ampl.display('c_end')
ampl.display(
"{m in M, (i,c) in C, t in T : c_progress[m,i,c,t] >= 1e-6} c_progress[m,i,c,t]"
)
Gurobi 12.0.0: Set parameter LogToConsole to value 1
tech:outlev = 1
Set parameter TimeLimit to value 150
lim:time = 150
Set parameter InfUnbdInfo to value 1
Gurobi Optimizer version 12.0.0 build v12.0.0rc1 (win64 - Windows 11.0 (26100.2))
CPU model: 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz, instruction set [SSE2|AVX|AVX2|AVX512]
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Non-default parameters:
TimeLimit 150
InfUnbdInfo 1
Warning: LP warm-starts, PStart/DStart, discarded due to model modification
Optimize a model with 8232 rows, 18465 columns and 22616 nonzeros
Model fingerprint: 0x836230f6
Model has 9424 simple general constraints
240 AND, 3888 OR, 5296 INDICATOR
Variable types: 1921 continuous, 16544 integer (0 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [3e-04, 1e+00]
Bounds range [1e+00, 6e+02]
RHS range [1e+00, 9e+00]
GenCon rhs range [1e-04, 9e+00]
GenCon coe range [1e+00, 1e+00]
User MIP start did not produce a new incumbent solution
User MIP start violates constraint R2 by 1.000000000
Presolve added 5742 rows and 0 columns
Presolve removed 0 rows and 13848 columns
Presolve time: 1.01s
Presolved: 13974 rows, 4617 columns, 74550 nonzeros
Variable types: 1927 continuous, 2690 integer (2690 binary)
Root relaxation: objective 1.028595e+02, 7121 iterations, 0.48 seconds (0.44 work units)
Another try with MIP start
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 102.85955 0 317 - 102.85955 - - 1s
0 0 102.86623 0 366 - 102.86623 - - 2s
0 0 102.86623 0 350 - 102.86623 - - 3s
0 0 102.97218 0 437 - 102.97218 - - 4s
0 0 103.03110 0 418 - 103.03110 - - 4s
0 0 103.24258 0 480 - 103.24258 - - 5s
0 0 103.26011 0 426 - 103.26011 - - 5s
0 0 103.33369 0 419 - 103.33369 - - 5s
0 0 103.35437 0 400 - 103.35437 - - 5s
H 0 0 218.3819508 103.35437 52.7% - 6s
0 0 103.37935 0 436 218.38195 103.37935 52.7% - 6s
H 0 0 206.3656789 103.37935 49.9% - 6s
H 0 0 189.3292899 103.37935 45.4% - 6s
0 0 103.40307 0 438 189.32929 103.40307 45.4% - 6s
0 0 103.43910 0 427 189.32929 103.43910 45.4% - 7s
H 0 0 184.3201183 103.43910 43.9% - 7s
0 0 103.44405 0 428 184.32012 103.44405 43.9% - 7s
0 0 103.46445 0 426 184.32012 103.46445 43.9% - 7s
H 0 0 181.3156805 103.46445 42.9% - 7s
H 0 0 166.3020710 103.46445 37.8% - 7s
0 0 103.46635 0 420 166.30207 103.46635 37.8% - 7s
0 0 103.46673 0 456 166.30207 103.46673 37.8% - 8s
H 0 0 163.2967456 103.46673 36.6% - 8s
H 0 0 163.2949704 103.46673 36.6% - 8s
H 0 0 162.2920119 103.46673 36.2% - 8s
0 0 103.46675 0 459 162.29201 103.46675 36.2% - 8s
0 0 103.51814 0 447 162.29201 103.51814 36.2% - 8s
H 0 0 161.2905325 103.52328 35.8% - 8s
0 0 103.53572 0 441 161.29053 103.53572 35.8% - 9s
0 0 103.56381 0 437 161.29053 103.56381 35.8% - 9s
H 0 0 148.2727811 103.56499 30.2% - 9s
H 0 0 148.2724852 103.56499 30.2% - 9s
H 0 0 147.2727811 103.56499 29.7% - 9s
0 0 103.56688 0 437 147.27278 103.56688 29.7% - 9s
0 0 103.56721 0 437 147.27278 103.56721 29.7% - 9s
H 0 0 141.2585799 103.56959 26.7% - 9s
0 0 103.56959 0 444 141.25858 103.56959 26.7% - 9s
0 0 103.57797 0 439 141.25858 103.57797 26.7% - 10s
H 0 0 140.2568047 103.57797 26.2% - 10s
H 0 0 139.2568047 103.57797 25.6% - 10s
0 0 103.57859 0 414 139.25680 103.57859 25.6% - 10s
0 0 103.58235 0 406 139.25680 103.58235 25.6% - 11s
H 0 0 138.2573964 103.58235 25.1% - 11s
0 0 103.58342 0 450 138.25740 103.58342 25.1% - 11s
0 0 103.60053 0 415 138.25740 103.60053 25.1% - 11s
0 0 103.60114 0 421 138.25740 103.60114 25.1% - 11s
0 0 103.60126 0 425 138.25740 103.60126 25.1% - 11s
0 0 103.60126 0 426 138.25740 103.60126 25.1% - 12s
0 0 103.60998 0 429 138.25740 103.60998 25.1% - 12s
0 0 103.61034 0 425 138.25740 103.61034 25.1% - 12s
0 0 103.61036 0 427 138.25740 103.61036 25.1% - 12s
0 0 103.61329 0 436 138.25740 103.61329 25.1% - 12s
0 0 103.61342 0 423 138.25740 103.61342 25.1% - 12s
0 0 103.61348 0 427 138.25740 103.61348 25.1% - 12s
0 0 103.63023 0 484 138.25740 103.63023 25.0% - 13s
0 0 103.63749 0 475 138.25740 103.63749 25.0% - 13s
0 0 103.63847 0 499 138.25740 103.63847 25.0% - 13s
0 0 103.63886 0 498 138.25740 103.63886 25.0% - 13s
0 0 103.63886 0 500 138.25740 103.63886 25.0% - 13s
0 0 103.64306 0 489 138.25740 103.64306 25.0% - 13s
0 0 103.64444 0 499 138.25740 103.64444 25.0% - 13s
0 0 103.64450 0 502 138.25740 103.64450 25.0% - 13s
0 0 103.64520 0 503 138.25740 103.64520 25.0% - 14s
0 0 103.64534 0 505 138.25740 103.64534 25.0% - 14s
0 0 103.64534 0 509 138.25740 103.64534 25.0% - 14s
0 0 103.64751 0 501 138.25740 103.64751 25.0% - 14s
0 0 103.64848 0 489 138.25740 103.64848 25.0% - 14s
0 0 103.64863 0 493 138.25740 103.64863 25.0% - 14s
0 0 103.64863 0 496 138.25740 103.64863 25.0% - 14s
0 0 103.65396 0 507 138.25740 103.65396 25.0% - 14s
0 0 103.65602 0 513 138.25740 103.65602 25.0% - 15s
0 0 103.67641 0 524 138.25740 103.67641 25.0% - 15s
0 0 103.68288 0 515 138.25740 103.68288 25.0% - 15s
0 0 103.69224 0 503 138.25740 103.69224 25.0% - 15s
0 0 103.69378 0 520 138.25740 103.69378 25.0% - 15s
0 0 103.69460 0 526 138.25740 103.69460 25.0% - 15s
0 0 103.69460 0 531 138.25740 103.69460 25.0% - 15s
0 0 103.69937 0 487 138.25740 103.69937 25.0% - 15s
H 0 0 138.2559172 103.69937 25.0% - 16s
H 0 0 137.2559172 103.69937 24.4% - 16s
0 0 103.70101 0 501 137.25592 103.70101 24.4% - 16s
0 0 103.70114 0 510 137.25592 103.70114 24.4% - 16s
0 0 103.70119 0 514 137.25592 103.70119 24.4% - 16s
0 0 103.70320 0 517 137.25592 103.70320 24.4% - 16s
0 0 103.70341 0 525 137.25592 103.70341 24.4% - 16s
0 0 103.70347 0 524 137.25592 103.70347 24.4% - 16s
0 0 103.71045 0 496 137.25592 103.71045 24.4% - 17s
0 0 103.71045 0 508 137.25592 103.71045 24.4% - 17s
0 0 103.71045 0 514 137.25592 103.71045 24.4% - 17s
0 0 103.71045 0 503 137.25592 103.71045 24.4% - 17s
0 0 103.71045 0 503 137.25592 103.71045 24.4% - 17s
0 0 103.71045 0 508 137.25592 103.71045 24.4% - 17s
0 0 103.71141 0 503 137.25592 103.71141 24.4% - 17s
0 0 103.71208 0 509 137.25592 103.71208 24.4% - 18s
0 0 103.71217 0 505 137.25592 103.71217 24.4% - 18s
0 0 103.72210 0 523 137.25592 103.72210 24.4% - 18s
0 0 103.72393 0 521 137.25592 103.72393 24.4% - 18s
0 0 103.72401 0 534 137.25592 103.72401 24.4% - 18s
0 0 103.75341 0 475 137.25592 103.75341 24.4% - 19s
0 0 103.75341 0 482 137.25592 103.75341 24.4% - 19s
0 0 103.75341 0 485 137.25592 103.75341 24.4% - 19s
0 0 103.75341 0 487 137.25592 103.75341 24.4% - 19s
0 0 103.75341 0 487 137.25592 103.75341 24.4% - 19s
H 0 0 134.2511834 103.75341 22.7% - 19s
0 0 103.75341 0 498 134.25118 103.75341 22.7% - 19s
H 0 0 131.2476331 103.75341 20.9% - 19s
0 0 103.75341 0 501 131.24763 103.75341 20.9% - 19s
H 0 0 130.2428994 103.75341 20.3% - 19s
H 0 0 130.2423077 103.75341 20.3% - 19s
0 0 103.79845 0 502 130.24231 103.79845 20.3% - 19s
0 0 103.79845 0 493 130.24231 103.79845 20.3% - 19s
0 0 103.79845 0 495 130.24231 103.79845 20.3% - 19s
0 0 103.80678 0 500 130.24231 103.80678 20.3% - 20s
0 0 103.80678 0 498 130.24231 103.80678 20.3% - 20s
H 0 0 128.2431953 103.80678 19.1% - 21s
0 2 103.80678 0 498 128.24320 103.80678 19.1% - 21s
H 47 49 127.2426036 104.08953 18.2% 542 22s
H 73 77 125.2378698 104.08953 16.9% 462 23s
H 283 266 125.2375740 104.08953 16.9% 218 24s
395 360 109.88807 36 160 125.23757 104.08953 16.9% 182 25s
H 445 394 123.2402367 104.08953 15.5% 172 25s
H 1406 1105 123.2396450 104.28971 15.4% 141 29s
1413 1176 107.99255 22 174 123.23964 104.28971 15.4% 140 30s
H 1900 1425 123.2387574 104.28971 15.4% 138 31s
1901 1426 106.48859 13 498 123.23876 104.28971 15.4% 138 36s
H 1902 1355 123.2375740 104.28971 15.4% 138 45s
H 1902 1287 123.2340237 104.28971 15.4% 138 45s
H 1902 1223 123.2337278 104.28971 15.4% 138 45s
H 1903 1162 123.2322486 104.28971 15.4% 137 49s
H 1903 1104 122.2322485 104.28971 14.7% 137 49s
1904 1105 105.68105 14 513 122.23225 104.28971 14.7% 137 51s
1911 1110 114.36390 34 525 122.23225 104.28971 14.7% 137 55s
1922 1117 119.52972 39 550 122.23225 104.28971 14.7% 136 60s
1924 1118 107.49412 19 550 122.23225 104.28971 14.7% 136 65s
H 1970 1095 122.2313609 104.40792 14.6% 161 69s
2013 1114 106.70194 22 276 122.23136 104.40792 14.6% 164 70s
H 2044 1068 121.2307692 104.40792 13.9% 166 71s
H 2047 1016 121.2304734 104.40792 13.9% 166 71s
2162 1048 105.33301 18 365 121.23047 104.50317 13.8% 175 75s
2411 1120 116.06077 35 135 121.23047 104.59638 13.7% 181 80s
2582 1193 109.35531 22 322 121.23047 104.73863 13.6% 182 85s
H 2735 1154 120.2298817 104.73863 12.9% 186 87s
3004 1242 107.52181 23 339 120.22988 104.83692 12.8% 191 90s
3342 1383 105.95072 24 314 120.22988 104.83692 12.8% 197 95s
3775 1418 114.61039 26 219 120.22988 104.83692 12.8% 203 100s
4170 1613 106.65029 19 337 120.22988 105.13755 12.6% 203 105s
4684 1721 106.49345 23 321 120.22988 105.14350 12.5% 206 110s
5064 1886 111.63191 26 264 120.22988 105.54463 12.2% 210 116s
5636 2205 infeasible 30 120.22988 105.81293 12.0% 213 121s
5993 2404 118.44381 42 145 120.22988 105.92202 11.9% 217 126s
6428 2623 114.77367 28 262 120.22988 105.99494 11.8% 220 130s
6900 2883 111.62970 27 228 120.22988 106.19207 11.7% 223 135s
7524 3180 107.41745 23 392 120.22988 106.31334 11.6% 223 140s
7802 3333 108.90406 27 209 120.22988 106.33400 11.6% 224 145s
7999 3456 infeasible 27 120.22988 106.37995 11.5% 227 150s
Cutting planes:
Gomory: 11
Lift-and-project: 1
Cover: 87
Implied bound: 27
Projected implied bound: 193
Clique: 4
MIR: 361
Flow cover: 224
Flow path: 2
GUB cover: 27
Inf proof: 6
Zero half: 17
RLT: 65
Relax-and-lift: 55
BQP: 10
PSD: 2
Explored 8278 nodes (1919604 simplex iterations) in 150.14 seconds (211.98 work units)
Thread count was 16 (of 16 available processors)
Solution count 10: 120.23 121.23 121.231 ... 123.239
Time limit reached
Best objective 1.202298816568e+02, best bound 1.063799512639e+02, gap 11.5195%
Gurobi 12.0.0: time limit, feasible solution; objective 120.2298817
1.9196e+06 simplex iterations
8278 branching nodes
absmipgap=13.8499, relmipgap=0.115195
c_progress[m,i,c,t] [1,1,*,*]
: 6 7 8 :=
2 5 . .
3 1 2 .
4 . 4 5
[1,2,*,*]
: 1 2 3 4 5 :=
1 6 3 . . .
2 . 3 3 . .
5 . . 3 4 .
6 . . . 2 2
7 . . . . 3
[2,1,*,*]
: 8 :=
6 3
7 3
[2,2,*,*]
: 3 :=
3 3
4 3
[2,3,*,*]
: 1 2 4 5 6 7 :=
1 3 . . . . .
2 4 3 . . . .
3 . 4 . . . .
4 . . 3 . . .
5 . . 4 4 . .
6 . . . 3 2 .
7 . . . . 3 .
8 . . . . 2 7
[3,1,*,*]
: 6 8 9 :=
1 8 . .
5 . 6 .
8 . 2 5
[3,2,8,7] 8
[3,4,*,*]
: 1 2 3 4 5 :=
1 3 . . . .
2 5 3 . . .
3 . 5 . . .
4 . . 3 . .
5 . . 5 4 .
6 . . . 4 2
7 . . . . 3
8 . . . . 3
;