Scheduling Multipurpose Batch Processes using State-Task Networks in Python#
Description: The State-Task Network (STN) is an approach to modeling multipurpose batch process for the purpose of short term scheduling. It was first developed by Kondili, et al., in 1993, and subsequently developed and extended by others.
Tags: state-task networks, gdp, disjunctive programming, batch processing
Notebook author: Jeffrey C. Kantor, Filipe Brandão <fdabrandao@gmail.com>
Based on: Original notebook from the ND Pyomo Cookbook
# Install dependencies
%pip install -q amplpy pandas numpy matplotlib networkx
# Google Colab & Kaggle integration
from amplpy import AMPL, ampl_notebook
ampl = ampl_notebook(
modules=["highs", "gurobi"], # modules to install
license_uuid="default", # license to use
) # instantiate AMPL object and register magics
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.display import display, HTML
SOLVER = "highs"
References#
Floudas, C. A., & Lin, X. (2005). Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research, 139(1), 131-162.
Harjunkoski, I., Maravelias, C. T., Bongers, P., Castro, P. M., Engell, S., Grossmann, I. E., … & Wassick, J. (2014). Scope for industrial applications of production scheduling models and solution methods. Computers & Chemical Engineering, 62, 161-193.
Kondili, E., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Computers & Chemical Engineering, 17(2), 211-227.
Méndez, C. A., Cerdá, J., Grossmann, I. E., Harjunkoski, I., & Fahl, M. (2006). State-of-the-art review of optimization methods for short-term scheduling of batch processes. Computers & Chemical Engineering, 30(6), 913-946.
Shah, N., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—II. Computational issues. Computers & Chemical Engineering, 17(2), 229-244.
Wassick, J. M., & Ferrio, J. (2011). Extending the resource task network for industrial applications. Computers & chemical engineering, 35(10), 2124-2140.
Example (Kondili, et al., 1993)#
A state-task network is a graphical representation of the activities in a multi-product batch process. The representation includes the minimum details needed for short term scheduling of batch operations.
A well-studied example due to Kondili (1993) is shown below. Other examples are available in the references cited above.
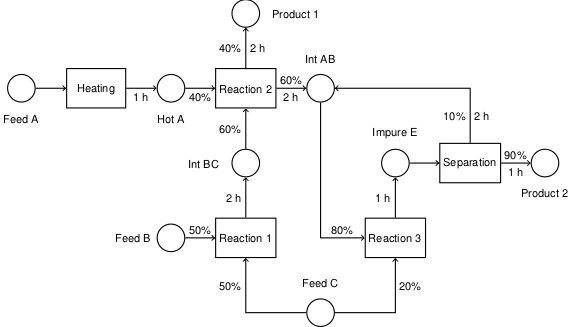
Each circular node in the diagram designates material in a particular state. The materials are generally held in suitable vessels with a known capacity. The relevant information for each state is the initial inventory, storage capacity, and the unit price of the material in each state. The price of materials in intermediate states may be assigned penalties in order to minimize the amount of work in progress.
The rectangular nodes denote process tasks. When scheduled for execution, each task is assigned an appropriate piece of equipment, and assigned a batch of material according to the incoming arcs. Each incoming arc begins at a state where the associated label indicates the mass fraction of the batch coming from that particular state. Outgoing arcs indicate the disposition of the batch to product states. The outgoing are labels indicate the fraction of the batch assigned to each product state, and the time necessary to produce that product.
Not shown in the diagram is the process equipment used to execute the tasks. A separate list of process units is available, each characterized by a capacity and list of tasks which can be performed in that unit.
Exercise#
Read this recipe for Hollandaise Sauce: http://www.foodnetwork.com/recipes/tyler-florence/hollandaise-sauce-recipe-1910043. Assume the available equipment consists of one sauce pan and a double-boiler on a stove. Draw a state-task network outlining the basic steps in the recipe.
Encoding the STN data#
The basic data structure specifies the states, tasks, and units comprising a state-task network. The intention is for all relevant problem data to be contained in a single JSON-like structure.
# planning horizon
H = 10
Kondili = {
# time grid
"TIME": range(0, H + 1),
# states
"STATES": {
"Feed_A": {"capacity": 500, "initial": 500, "price": 0},
"Feed_B": {"capacity": 500, "initial": 500, "price": 0},
"Feed_C": {"capacity": 500, "initial": 500, "price": 0},
"Hot_A": {"capacity": 100, "initial": 0, "price": -100},
"Int_AB": {"capacity": 200, "initial": 0, "price": -100},
"Int_BC": {"capacity": 150, "initial": 0, "price": -100},
"Impure_E": {"capacity": 100, "initial": 0, "price": -100},
"Product_1": {"capacity": 500, "initial": 0, "price": 10},
"Product_2": {"capacity": 500, "initial": 0, "price": 10},
},
# state-to-task arcs indexed by (state, task)
"ST_ARCS": {
("Feed_A", "Heating"): {"rho": 1.0},
("Feed_B", "Reaction_1"): {"rho": 0.5},
("Feed_C", "Reaction_1"): {"rho": 0.5},
("Feed_C", "Reaction_3"): {"rho": 0.2},
("Hot_A", "Reaction_2"): {"rho": 0.4},
("Int_AB", "Reaction_3"): {"rho": 0.8},
("Int_BC", "Reaction_2"): {"rho": 0.6},
("Impure_E", "Separation"): {"rho": 1.0},
},
# task-to-state arcs indexed by (task, state)
"TS_ARCS": {
("Heating", "Hot_A"): {"dur": 1, "rho": 1.0},
("Reaction_2", "Product_1"): {"dur": 2, "rho": 0.4},
("Reaction_2", "Int_AB"): {"dur": 2, "rho": 0.6},
("Reaction_1", "Int_BC"): {"dur": 2, "rho": 1.0},
("Reaction_3", "Impure_E"): {"dur": 1, "rho": 1.0},
("Separation", "Int_AB"): {"dur": 2, "rho": 0.1},
("Separation", "Product_2"): {"dur": 1, "rho": 0.9},
},
# unit data indexed by (unit, task)
"UNIT_TASKS": {
("Heater", "Heating"): {
"Bmin": 0,
"Bmax": 100,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_1"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_2"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_3"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_1"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_2"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_3"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Still", "Separation"): {
"Bmin": 0,
"Bmax": 200,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
},
}
H = 16
Hydrolubes = {
# time grid
"TIME": range(0, H + 1),
# states
"STATES": {
"Feed_A": {"capacity": 500, "initial": 500, "price": 0},
"Feed_B": {"capacity": 500, "initial": 500, "price": 0},
"Feed_C": {"capacity": 500, "initial": 500, "price": 0},
"Hot_A": {"capacity": 100, "initial": 0, "price": -100},
"Int_AB": {"capacity": 200, "initial": 0, "price": -100},
"Int_BC": {"capacity": 150, "initial": 0, "price": -100},
"Impure_E": {"capacity": 100, "initial": 0, "price": -100},
"Product_1": {"capacity": 500, "initial": 0, "price": 10},
"Product_2": {"capacity": 500, "initial": 0, "price": 10},
},
# state-to-task arcs indexed by (state, task)
"ST_ARCS": {
("Feed_A", "Heating"): {"rho": 1.0},
("Feed_B", "Reaction_1"): {"rho": 0.5},
("Feed_C", "Reaction_1"): {"rho": 0.5},
("Feed_C", "Reaction_3"): {"rho": 0.2},
("Hot_A", "Reaction_2"): {"rho": 0.4},
("Int_AB", "Reaction_3"): {"rho": 0.8},
("Int_BC", "Reaction_2"): {"rho": 0.6},
("Impure_E", "Separation"): {"rho": 1.0},
},
# task-to-state arcs indexed by (task, state)
"TS_ARCS": {
("Heating", "Hot_A"): {"dur": 1, "rho": 1.0},
("Reaction_2", "Product_1"): {"dur": 2, "rho": 0.4},
("Reaction_2", "Int_AB"): {"dur": 2, "rho": 0.6},
("Reaction_1", "Int_BC"): {"dur": 2, "rho": 1.0},
("Reaction_3", "Impure_E"): {"dur": 1, "rho": 1.0},
("Separation", "Int_AB"): {"dur": 2, "rho": 0.1},
("Separation", "Product_2"): {"dur": 1, "rho": 0.9},
},
# unit data indexed by (unit, task)
"UNIT_TASKS": {
("Heater", "Heating"): {
"Bmin": 0,
"Bmax": 100,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_1"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_2"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_1", "Reaction_3"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_1"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_2"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Reactor_2", "Reaction_3"): {
"Bmin": 0,
"Bmax": 80,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
("Still", "Separation"): {
"Bmin": 0,
"Bmax": 200,
"Cost": 1,
"vCost": 0,
"Tclean": 0,
},
},
}
import matplotlib.pyplot as plt
import networkx as nx
def remove_isolated_states(stn, verbose=False):
states = set()
for state in stn["STATES"]:
states.add(state)
tasks = set()
connected_tasks = set()
connected_states = set()
for s, t in stn["ST_ARCS"]:
tasks.add(t)
if s not in states:
continue
connected_tasks.add(t)
connected_states.add(s)
for t, s in stn["TS_ARCS"]:
tasks.add(t)
if s not in states:
continue
connected_tasks.add(t)
connected_states.add(s)
units = set()
connected_units = set()
tasks_with_units = set()
for u, t in stn["UNIT_TASKS"]:
units.add(u)
tasks_with_units.add(t)
if t not in connected_tasks:
continue
connected_units.add(u)
if verbose:
print(f"isolated satates: {states-connected_states}")
print(f"isolated tasks: {tasks-connected_tasks}")
print(f"isolated units: {units-connected_units}")
print(f"tasks without units: {tasks-tasks_with_units}")
return (
{
# time grid
"TIME": stn["TIME"],
# states
"STATES": {s: stn["STATES"][s] for s in connected_states},
# state-to-task arcs indexed by (state, task)
"ST_ARCS": {
(s, t): stn["ST_ARCS"][(s, t)]
for (s, t) in stn["ST_ARCS"]
if s in connected_states and t in connected_tasks
},
# task-to-state arcs indexed by (task, state)
"TS_ARCS": {
(t, s): stn["TS_ARCS"][(t, s)]
for (t, s) in stn["TS_ARCS"]
if s in connected_states and t in connected_tasks
},
# unit data indexed by (unit, task)
"UNIT_TASKS": {
(u, t): stn["UNIT_TASKS"][(u, t)]
for (u, t) in stn["UNIT_TASKS"]
if t in connected_tasks
},
},
connected_states,
connected_tasks,
)
def build_graph(stn, verbose=False):
# Remove isolated nodes
stn, connected_states, connected_tasks = remove_isolated_states(
stn, verbose=verbose
)
# Create a directed graph
graph = nx.DiGraph()
# Add states and tasks as nodes
graph.add_nodes_from(connected_states, type="state")
graph.add_nodes_from(connected_tasks, type="task")
# Add state-to-task and task-to-state arcs
for (s, t), v in stn["ST_ARCS"].items():
if s not in connected_states or t not in connected_tasks:
continue
graph.add_edge(s, t, rho=v["rho"])
for (t, s), v in stn["TS_ARCS"].items():
if s not in connected_states or t not in connected_tasks:
continue
graph.add_edge(t, s, rho=v["rho"])
return stn, graph
def draw_graph(stn, graph, with_labels=False, verbose=False):
# Determine initial and final states
initial_states = {
state
for state, attr in stn["STATES"].items()
if attr["initial"] > 0 and graph.in_degree(state) == 0
}
final_states = {state for state in stn["STATES"] if graph.out_degree(state) == 0}
if verbose:
print(f"initial states: {initial_states}")
print(f"final states: {final_states}")
tasks = set()
for s, t in stn["ST_ARCS"]:
tasks.add(t)
for t, s in stn["TS_ARCS"]:
tasks.add(t)
# Position nodes
initial_x = 0.1
intermediate_x = 0.5
final_x = 0.9
y = 0.5
new_pos = {}
for node in graph.nodes():
if node in initial_states:
new_pos[node] = (initial_x, y)
initial_x += 0.1
elif node in final_states:
new_pos[node] = (final_x, y)
final_x -= 0.1
else:
new_pos[node] = (intermediate_x, y)
intermediate_x += 0.1
# Adjust positions of tasks based on their connected states
task_y_offset = 0.2
for node in tasks:
avg_x = sum(
new_pos[pred][0] for pred in graph.predecessors(node)
) / graph.in_degree(node)
new_pos[node] = (avg_x, y - task_y_offset)
# Draw the network graph
plt.figure(figsize=(14, 8))
node_colors = [
(
"yellow"
if n in initial_states
else (
"red"
if n in final_states
else "skyblue" if graph.nodes[n]["type"] == "state" else "lightgreen"
)
)
for n in graph.nodes()
]
nx.draw(
graph,
new_pos,
with_labels=with_labels,
node_color=node_colors,
node_size=100,
font_size=9,
font_weight="bold",
arrowstyle="-|>",
arrowsize=20,
)
edge_labels = nx.get_edge_attributes(graph, "rho")
if with_labels:
nx.draw_networkx_edge_labels(
graph, new_pos, edge_labels=edge_labels, font_color="red"
)
plt.title("Network Graph with Spatially Separated Initial and Final States")
plt.show()
initial_stn = Hydrolubes # Hydrolubes, Kondili
full_stn, full_graph = build_graph(initial_stn, verbose=False)
draw_graph(full_stn, full_graph, with_labels=True, verbose=False)

def list_predecessors(stn, graph, node, visited=set(), depth=0, verbose=False):
visited.add(node)
pred = list(graph.predecessors(node))
if verbose:
print(
" " * depth,
node,
graph.nodes[node]["type"],
"->",
[(p, graph.edges[p, node]["rho"]) for p in pred],
)
for p in pred:
list_predecessors(stn, graph, p, visited, depth + 1, verbose)
return visited
def clean_stn(stn, graph, target, verbose=False):
visited = list_predecessors(stn, graph, target, verbose=verbose)
return {
# time grid
"TIME": stn["TIME"],
# states
"STATES": {s: stn["STATES"][s] for s in stn["STATES"] if s in visited},
# state-to-task arcs indexed by (state, task)
"ST_ARCS": {
(s, t): stn["ST_ARCS"][(s, t)]
for (s, t) in stn["ST_ARCS"]
if s in visited and t in visited
},
# task-to-state arcs indexed by (task, state)
"TS_ARCS": {
(t, s): stn["TS_ARCS"][(t, s)]
for (t, s) in stn["TS_ARCS"]
if s in visited and t in visited
},
# unit data indexed by (unit, task)
"UNIT_TASKS": {
(u, t): stn["UNIT_TASKS"][(u, t)]
for (u, t) in stn["UNIT_TASKS"]
if t in visited
},
}
stn = clean_stn(full_stn, full_graph, "Product_1", verbose=False)
filtered_stn, filtered_graph = build_graph(stn)
draw_graph(filtered_stn, filtered_graph, with_labels=True)

STN = full_stn # filtered_stn or full_stn
TIME = STN["TIME"]
unit_tasks_pd = pd.DataFrame.from_dict(STN["UNIT_TASKS"], orient="index")
states_df = pd.DataFrame.from_dict(STN["STATES"], orient="index")
Setting a time grid#
The following computations can be done on any time grid, including real-valued time points. TIME is a list of time points commencing at 0.
Creating an AMPL model#
The following AMPL model closely follows the development in Kondili, et al. (1993). In particular, the first step in the model is to process the STN data to create sets as given in Kondili.
One important difference from Kondili is the adoption of a more natural time scale that starts at \(t = 0\) and extends to \(t = H\) (rather than from 1 to H+1).
A second difference is the introduction of an additional decision variable denoted by \(Q_{j,t}\) indicating the amount of material in unit \(j\) at time \(t\). A material balance then reads
Following Kondili’s notation, \(I_j\) is the set of tasks that can be performed in unit \(j\), and \(\bar{S}_i\) is the set of states fed by task \(j\). We assume the units are empty at the beginning and end of production period, i.e.,
The unit allocation constraints are written the full backward aggregation method described by Shah (1993). The allocation constraint reads
Each processing unit \(j\) is tagged with a minimum and maximum capacity, \(B_{ij}^{min}\) and \(B_{ij}^{max}\), respectively, denoting the minimum and maximum batch sizes for each task \(i\). A minimum capacity may be needed to cover heat exchange coils in a reactor or mixing blades in a blender, for example. The capacity may depend on the nature of the task being performed. These constraints are written
Characterization of tasks#
STATES = STN["STATES"]
ST_ARCS = STN["ST_ARCS"]
TS_ARCS = STN["TS_ARCS"]
UNIT_TASKS = STN["UNIT_TASKS"]
TIME = STN["TIME"]
H = max(TIME)
# set of tasks
TASKS = set([i for (j, i) in UNIT_TASKS])
# S[i] input set of states which feed task i
S = {i: set() for i in TASKS}
for s, i in ST_ARCS:
S[i].add(s)
# S_[i] output set of states fed by task i
S_ = {i: set() for i in TASKS}
for i, s in TS_ARCS:
S_[i].add(s)
# rho[(i,s)] input fraction of task i from state s
rho = {(i, s): ST_ARCS[(s, i)]["rho"] for (s, i) in ST_ARCS}
# rho_[(i,s)] output fraction of task i to state s
rho_ = {(i, s): TS_ARCS[(i, s)]["rho"] for (i, s) in TS_ARCS}
# P[(i,s)] time for task i output to state s
P = {(i, s): TS_ARCS[(i, s)]["dur"] for (i, s) in TS_ARCS}
# p[i] completion time for task i
p = {i: max([P[(i, s)] for s in S_[i]]) for i in TASKS}
# K[i] set of units capable of task i
K = {i: set() for i in TASKS}
for j, i in UNIT_TASKS:
K[i].add(j)
Characterization of states#
# T[s] set of tasks receiving material from state s
T = {s: set() for s in STATES}
for s, i in ST_ARCS:
T[s].add(i)
# set of tasks producing material for state s
T_ = {s: set() for s in STATES}
for i, s in TS_ARCS:
T_[s].add(i)
# C[s] storage capacity for state s
C = {s: STATES[s]["capacity"] for s in STATES}
Characterization of units#
UNITS = list(sorted(set([j for (j, i) in UNIT_TASKS])))
# I[j] set of tasks performed with unit j
I = {j: set() for j in UNITS}
for j, i in UNIT_TASKS:
I[j].add(i)
# Bmax[(i,j)] maximum capacity of unit j for task i
Bmax = {(i, j): UNIT_TASKS[(j, i)]["Bmax"] for (j, i) in UNIT_TASKS}
# Bmin[(i,j)] minimum capacity of unit j for task i
Bmin = {(i, j): UNIT_TASKS[(j, i)]["Bmin"] for (j, i) in UNIT_TASKS}
AMPL model#
%%writefile batch_process.mod
set TASKS;
set UNITS;
set TIME;
param H; # End time or horizon
set STATES;
param price{STATES};
param initial{STATES};
set I{j in UNITS}; # I[j] set of tasks performed with unit j
set K{i in TASKS}; # K[i] set of units capable of task i
set S_In{i in TASKS}; # S_In[i] input set of states which feed task i
set S_Out{i in TASKS}; # S_Out[i] output set of states fed by task i
set T_In{s in STATES}; # T_In[s] set of tasks producing material for state s
set T_Out{s in STATES}; # T_Out[s] set of tasks receiving material from state s
param P{i in TASKS, s in S_Out[i]}; # P[i,s] time for task i output to state s
param p{i in TASKS}; # Processing times for tasks
param Tclean{(j,i) in UNITS cross TASKS};
param C{s in STATES}; # Capacity constraints for states
param rho_in{i in TASKS, s in S_In[i]}; # rho_in[i,s] input fraction of task i from state s
param rho_out{i in TASKS, s in S_Out[i]}; # rho_out[i,s] output fraction of task i to state s
param Bmin{(i,j) in UNITS cross TASKS};
param Bmax{(i,j) in UNITS cross TASKS};
param Cost{(i,j) in UNITS cross TASKS} > 0;
param vCost{(i,j) in UNITS cross TASKS} > 0;
# W[i,j,t] 1 if task i starts in unit j at time t
var W{i in TASKS, j in K[i], t in TIME} binary;
# B[i,j,t] size of batch assigned to task i in unit j at time t
var B{i in TASKS, j in K[i], t in TIME} >= 0;
# S[s,t] inventory of state s at time t
var S{s in STATES, t in TIME} >= 0, <= C[s];
# Q[j,t] inventory of unit j at time t
var Q{j in UNITS, t in TIME} >= 0;
# Objective function
var TotalValue = sum{s in STATES} price[s] * S[s,H];
var TotalCost = sum{i in TASKS, j in K[i], t in TIME} (Cost[j,i] * W[i,j,t] + vCost[j,i] * B[i,j,t]);;
# Objective function
maximize Total_Profit: TotalValue - TotalCost;
# Constraints
# a unit can only be allocated to one task
subject to Unit_Allocation{j in UNITS, t in TIME}:
sum{i in I[j], tprime in TIME: tprime >= (t - p[i] + 1 - Tclean[j,i]) && tprime <= t} W[i,j,tprime] <= 1;
# state mass balances
subject to State_Balance{s in STATES, t in TIME}:
S[s,t] = (if t > 0 then S[s,t-1] else initial[s])
+ sum {i in T_In[s], j in K[i]: t >= P[i,s]} rho_out[i,s]*B[i,j,t-P[i,s]]
- sum {i in T_Out[s], j in K[i]} rho_in[i,s] * B[i,j,t];
# unit capacity constraints
subject to Unit_Capacity_Min{i in TASKS, j in K[i], t in TIME}:
W[i,j,t]*Bmin[j,i] <= B[i,j,t];
subject to Unit_Capacity_Max{i in TASKS, j in K[i], t in TIME}:
B[i,j,t] <= W[i,j,t]*Bmax[j,i];
# unit mass balances
subject to Unit_Balance{j in UNITS, t in TIME}:
Q[j,t] = (if t > 0 then Q[j,t-1] else 0)
+ sum {i in I[j]} B[i,j,t]
- sum {i in I[j], s in S_Out[i]: t >= P[i,s]} rho_out[i,s] * B[i,j,t-P[i,s]];
# unit terminal condition
subject to Terminal_Condition{j in UNITS}:
Q[j,H] = 0;
Writing batch_process.mod
ampl = AMPL()
ampl.read("batch_process.mod")
TIME = np.array(TIME)
ampl.set["TIME"] = TIME
ampl.set["TASKS"] = TASKS
ampl.set["UNITS"] = UNITS
ampl.set["STATES"] = STATES.keys()
ampl.set["I"] = I
ampl.set["K"] = K
ampl.set["T_In"] = T_
ampl.set["T_Out"] = T
ampl.set["S_In"] = S
ampl.set["S_Out"] = S_
ampl.param["H"] = H
ampl.param["price"] = states_df[["price"]]
ampl.param["initial"] = states_df[["initial"]]
ampl.param["P"] = P
ampl.param["p"] = p
ampl.param["C"] = states_df[["capacity"]]
ampl.param["rho_in"] = rho
ampl.param["rho_out"] = rho_
ampl.param["Bmin"] = unit_tasks_pd[["Bmin"]]
ampl.param["Bmax"] = unit_tasks_pd[["Bmax"]]
ampl.param["Cost"] = unit_tasks_pd[["Cost"]]
ampl.param["vCost"] = unit_tasks_pd[["vCost"]]
ampl.param["Tclean"] = unit_tasks_pd[["Tclean"]]
# ampl.option["presolve_logfile"] = "presolve.log"
# ampl.option["presolve"] = 0
if SOLVER == "highs":
ampl.solve(solver="highs", highs_options="outlev=1")
elif SOLVER == "gurobi":
ampl.solve(solver="gurobi", gurobi_options="outlev=1 iis=1 timelim=600")
elif SOLVER == "cplex":
ampl.solve(
solver="cplexmp",
highs_options="outlev=1",
cplex_options="outlev=1 iis=1 timelim=30",
)
assert ampl.solve_result in ["solved", "limit", "infeasible"], ampl.solve_result
HiGHS 1.7.0: tech:outlev = 1
Running HiGHS 1.7.0 (git hash: 50670fd): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [1e-01, 2e+02]
Cost [1e+00, 1e+02]
Bound [1e+00, 5e+02]
RHS [1e+00, 5e+02]
Presolving model
341 rows, 413 cols, 1316 nonzeros 0s
268 rows, 340 cols, 1151 nonzeros 0s
220 rows, 293 cols, 881 nonzeros 0s
194 rows, 255 cols, 757 nonzeros 0s
Solving MIP model with:
194 rows
255 cols (100 binary, 0 integer, 0 implied int., 155 continuous)
757 nonzeros
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
0 0 0 0.00% 10000 -inf inf 0 0 0 0 0.0s
R 0 0 0 0.00% 4923.399757 3303.666667 49.03% 0 0 0 238 0.0s
C 0 0 0 0.00% 4919.574236 3898 26.21% 329 40 0 310 0.1s
L 0 0 0 0.00% 4901.716371 4870.333333 0.64% 1247 88 0 586 0.4s
L 0 0 0 0.00% 4901.673117 4870.333333 0.64% 1302 93 0 1191 0.5s
19.0% inactive integer columns, restarting
Model after restart has 161 rows, 215 cols (81 bin., 0 int., 0 impl., 134 cont.), and 615 nonzeros
0 0 0 0.00% 4901.673117 4870.333333 0.64% 29 0 0 1485 0.5s
0 0 0 0.00% 4901.673117 4870.333333 0.64% 29 26 3 1585 0.5s
L 0 0 0 0.00% 4896.157012 4870.333333 0.53% 976 81 3 1893 1.1s
L 0 0 0 0.00% 4896.157012 4870.333333 0.53% 976 81 3 3130 1.4s
Symmetry detection completed in 0.0s
Found 5 generators
L 0 0 0 0.00% 4896.157012 4870.333333 0.53% 976 31 3 3763 1.8s
Solving report
Status Optimal
Primal bound 4870.33333333
Dual bound 4870.81944444
Gap 0.00998% (tolerance: 0.01%)
Solution status feasible
4870.33333333 (objective)
0 (bound viol.)
1.07802655691e-13 (int. viol.)
0 (row viol.)
Timing 2.32 (total)
0.01 (presolve)
0.00 (postsolve)
Nodes 173
LP iterations 7978 (total)
2037 (strong br.)
886 (separation)
3465 (heuristics)
HiGHS 1.7.0: optimal solution; objective 4870.333333
7978 simplex iterations
173 branching nodes
absmipgap=0.486111, relmipgap=9.98106e-05
# %load_ext google.colab.data_table
if ampl.solve_result == "infeasible":
var_iis, con_iis = ampl.get_iis()
print("var_iis:", var_iis)
print("con_iis:", con_iis)
else:
solution = ampl.get_solution()
print("solution:", solution)
solution: {"W['Reaction_1','Reactor_2',0]": 1, "W['Reaction_1','Reactor_2',4]": -4.973799150320706e-15, "W['Reaction_1','Reactor_2',5]": 1, "W['Reaction_1','Reactor_2',9]": 9.947598300641404e-16, "W['Reaction_1','Reactor_1',0]": 1, "W['Reaction_1','Reactor_1',4]": -2.615241356807019e-14, "W['Reaction_1','Reactor_1',5]": 8.688161301506626e-14, "W['Reaction_1','Reactor_1',6]": 0.9999999999998922, "W['Reaction_1','Reactor_1',9]": 1.978625596699146e-14, "W['Separation','Still',5]": 6.389999640532549e-14, "W['Separation','Still',8]": 1, "W['Separation','Still',11]": 1, "W['Separation','Still',14]": 1, "W['Reaction_3','Reactor_2',4]": 0.9999999999999983, "W['Reaction_3','Reactor_2',7]": 1, "W['Reaction_3','Reactor_2',10]": 1, "W['Reaction_3','Reactor_2',13]": 1, "W['Reaction_3','Reactor_1',4]": 8.688161301506626e-14, "W['Reaction_3','Reactor_1',7]": 8.693046282814976e-14, "W['Reaction_3','Reactor_1',8]": 1.978625596699146e-14, "W['Reaction_3','Reactor_1',10]": 0.9999999999999803, "W['Reaction_3','Reactor_1',13]": 1, "W['Heating','Heater',1]": 1, "W['Heating','Heater',5]": 1, "W['Heating','Heater',7]": 1, "W['Reaction_2','Reactor_2',2]": 1, "W['Reaction_2','Reactor_2',4]": 6.59472476627343e-15, "W['Reaction_2','Reactor_2',8]": 0.999999999999999, "W['Reaction_2','Reactor_2',11]": 1, "W['Reaction_2','Reactor_1',2]": 1, "W['Reaction_2','Reactor_1',4]": 0.9999999999999393, "W['Reaction_2','Reactor_1',6]": 2.08425869156296e-14, "W['Reaction_2','Reactor_1',8]": 0.9999999999999803, "W['Reaction_2','Reactor_1',11]": 1, "B['Reaction_1','Reactor_2',0]": 80, "B['Reaction_1','Reactor_2',5]": 80, "B['Reaction_1','Reactor_2',9]": 7.958078640513123e-14, "B['Reaction_1','Reactor_1',0]": 80, "B['Reaction_1','Reactor_1',4]": -2.092193085445615e-12, "B['Reaction_1','Reactor_1',5]": 6.9505290412053e-12, "B['Reaction_1','Reactor_1',6]": 79.99999999999137, "B['Reaction_1','Reactor_1',9]": 1.588229547877518e-12, "B['Separation','Still',5]": 5.115907697472721e-12, "B['Separation','Still',8]": 160.0000000000086, "B['Separation','Still',11]": 160, "B['Separation','Still',14]": 120, "B['Reaction_3','Reactor_2',4]": 79.99999999999987, "B['Reaction_3','Reactor_2',7]": 80, "B['Reaction_3','Reactor_2',10]": 80, "B['Reaction_3','Reactor_2',13]": 39.99999999999996, "B['Reaction_3','Reactor_1',4]": 6.9505290412053e-12, "B['Reaction_3','Reactor_1',7]": 6.954437026251981e-12, "B['Reaction_3','Reactor_1',8]": 1.582900477359317e-12, "B['Reaction_3','Reactor_1',10]": 79.99999999999842, "B['Reaction_3','Reactor_1',13]": 80, "B['Heating','Heater',1]": 95.99999999999866, "B['Heating','Heater',5]": 17.33333333332865, "B['Heating','Heater',6]": -2.886579864025406e-14, "B['Heating','Heater',7]": 99.99999999999993, "B['Reaction_2','Reactor_2',2]": 80, "B['Reaction_2','Reactor_2',4]": 5.275779813018744e-13, "B['Reaction_2','Reactor_2',8]": 79.99999999999991, "B['Reaction_2','Reactor_2',11]": 53.33333333333329, "B['Reaction_2','Reactor_1',2]": 80, "B['Reaction_2','Reactor_1',4]": 79.99999999999514, "B['Reaction_2','Reactor_1',6]": 1.667406953250368e-12, "B['Reaction_2','Reactor_1',8]": 79.99999999999842, "B['Reaction_2','Reactor_1',11]": 80, "S['Feed_B',0]": 420, "S['Feed_B',1]": 420, "S['Feed_B',2]": 420, "S['Feed_B',3]": 420, "S['Feed_B',4]": 420.000000000001, "S['Feed_B',5]": 379.9999999999976, "S['Feed_B',6]": 340.0000000000019, "S['Feed_B',7]": 340.0000000000019, "S['Feed_B',8]": 340.0000000000019, "S['Feed_B',9]": 340.000000000001, "S['Feed_B',10]": 340.000000000001, "S['Feed_B',11]": 340.000000000001, "S['Feed_B',12]": 340.000000000001, "S['Feed_B',13]": 340.000000000001, "S['Feed_B',14]": 340.000000000001, "S['Feed_B',15]": 340.000000000001, "S['Feed_B',16]": 340.000000000001, "S['Int_BC',2]": 64, "S['Int_BC',3]": 64, "S['Int_BC',4]": 16.0000000000026, "S['Int_BC',5]": 16.0000000000026, "S['Int_BC',6]": 15.99999999999911, "S['Int_BC',7]": 96.00000000000605, "S['Int_BC',8]": 79.99999999999831, "S['Int_BC',9]": 79.99999999999831, "S['Int_BC',10]": 79.9999999999983, "S['Hot_A',2]": 31.99999999999866, "S['Hot_A',3]": 31.99999999999866, "S['Hot_A',4]": 3.929301328753354e-13, "S['Hot_A',6]": 17.33333333333276, "S['Hot_A',7]": 17.33333333333273, "S['Hot_A',8]": 53.33333333333331, "S['Hot_A',9]": 53.33333333333331, "S['Hot_A',10]": 53.33333333333331, "S['Impure_E',5]": 80.0000000000017, "S['Impure_E',6]": 80.0000000000017, "S['Impure_E',7]": 80.0000000000017, "S['Impure_E',9]": 1.582900477359317e-12, "S['Impure_E',10]": 1.582900477359317e-12, "S['Product_1',4]": 64, "S['Product_1',5]": 64, "S['Product_1',6]": 95.99999999999825, "S['Product_1',7]": 95.99999999999825, "S['Product_1',8]": 95.99999999999892, "S['Product_1',9]": 95.99999999999892, "S['Product_1',10]": 159.9999999999983, "S['Product_1',11]": 159.9999999999983, "S['Product_1',12]": 159.9999999999983, "S['Product_1',13]": 213.3333333333316, "S['Product_1',14]": 213.3333333333316, "S['Product_1',15]": 213.3333333333316, "S['Product_1',16]": 213.3333333333316, "S['Product_2',6]": 4.604316927725449e-12, "S['Product_2',7]": 4.604316927725449e-12, "S['Product_2',8]": 4.604316927725449e-12, "S['Product_2',9]": 144.0000000000124, "S['Product_2',10]": 144.0000000000124, "S['Product_2',11]": 144.0000000000124, "S['Product_2',12]": 288.0000000000124, "S['Product_2',13]": 288.0000000000124, "S['Product_2',14]": 288.0000000000124, "S['Product_2',15]": 396.0000000000124, "S['Product_2',16]": 396.0000000000124, "S['Feed_A',0]": 500, "S['Feed_A',1]": 404.0000000000013, "S['Feed_A',2]": 404.0000000000013, "S['Feed_A',3]": 404.0000000000013, "S['Feed_A',4]": 404.0000000000013, "S['Feed_A',5]": 386.6666666666727, "S['Feed_A',6]": 386.6666666666727, "S['Feed_A',7]": 286.6666666666728, "S['Feed_A',8]": 286.6666666666728, "S['Feed_A',9]": 286.6666666666728, "S['Feed_A',10]": 286.6666666666728, "S['Feed_A',11]": 286.6666666666728, "S['Feed_A',12]": 286.6666666666728, "S['Feed_A',13]": 286.6666666666728, "S['Feed_A',14]": 286.6666666666728, "S['Feed_A',15]": 286.6666666666728, "S['Feed_A',16]": 286.6666666666728, "S['Int_AB',4]": 31.99999999999454, "S['Int_AB',5]": 31.99999999999454, "S['Int_AB',6]": 79.99999999999194, "S['Int_AB',7]": 15.99999999999908, "S['Int_AB',8]": 15.99999999999882, "S['Int_AB',9]": 15.99999999999882, "S['Int_AB',16]": 12, "S['Feed_C',0]": 420, "S['Feed_C',1]": 420, "S['Feed_C',2]": 420, "S['Feed_C',3]": 420, "S['Feed_C',4]": 403.9999999999997, "S['Feed_C',5]": 363.9999999999962, "S['Feed_C',6]": 324.0000000000005, "S['Feed_C',7]": 307.9999999999991, "S['Feed_C',8]": 307.9999999999988, "S['Feed_C',9]": 307.999999999998, "S['Feed_C',10]": 275.9999999999983, "S['Feed_C',11]": 275.9999999999983, "S['Feed_C',12]": 275.9999999999983, "S['Feed_C',13]": 251.9999999999983, "S['Feed_C',14]": 251.9999999999983, "S['Feed_C',15]": 251.9999999999983, "S['Feed_C',16]": 251.9999999999983, "Q['Heater',1]": 95.99999999999866, "Q['Heater',5]": 17.33333333332865, "Q['Heater',6]": -2.886579864025406e-14, "Q['Heater',7]": 99.99999999999993, "Q['Reactor_1',0]": 80, "Q['Reactor_1',1]": 80, "Q['Reactor_1',2]": 80, "Q['Reactor_1',3]": 80, "Q['Reactor_1',4]": 80, "Q['Reactor_1',5]": 80, "Q['Reactor_1',6]": 79.99999999999999, "Q['Reactor_1',7]": 80, "Q['Reactor_1',8]": 80, "Q['Reactor_1',9]": 80.00000000000001, "Q['Reactor_1',10]": 80.00000000000001, "Q['Reactor_1',11]": 80, "Q['Reactor_1',12]": 80, "Q['Reactor_1',13]": 80, "Q['Reactor_2',0]": 80, "Q['Reactor_2',1]": 80, "Q['Reactor_2',2]": 80, "Q['Reactor_2',3]": 80, "Q['Reactor_2',4]": 80.0000000000004, "Q['Reactor_2',5]": 80.00000000000053, "Q['Reactor_2',6]": 80, "Q['Reactor_2',7]": 80, "Q['Reactor_2',8]": 79.99999999999991, "Q['Reactor_2',9]": 80, "Q['Reactor_2',10]": 80.00000000000009, "Q['Reactor_2',11]": 53.33333333333329, "Q['Reactor_2',12]": 53.33333333333329, "Q['Reactor_2',13]": 39.99999999999996, "Q['Still',5]": 5.115907697472721e-12, "Q['Still',6]": 5.11590769747272e-13, "Q['Still',8]": 160.0000000000086, "Q['Still',9]": 16.00000000000086, "Q['Still',11]": 160, "Q['Still',12]": 16, "Q['Still',14]": 120, "Q['Still',15]": 11.99999999999999, 'TotalValue': 4893.333333333439, 'TotalCost': 23.000000000000153}
assert ampl.solve_result in ["solved", "limit"], ampl.solve_result
Analysis#
Profitability#
total_value, total_cost = ampl.get_value("TotalValue"), ampl.get_value("TotalCost")
print("Value of State Inventories = {0:12.2f}".format(total_value))
print(" Cost of Unit Assignments = {0:12.2f}".format(total_cost))
print(" Net Objective = {0:12.2f}".format(total_value - total_cost))
Value of State Inventories = 4893.33
Cost of Unit Assignments = 23.00
Net Objective = 4870.33
Unit assignment#
solution = ampl.get_solution(flat=False, zeros=True)
# solution = {
# "W": ampl.var["W"].to_dict(),
# "B": ampl.var["B"].to_dict(),
# "S": ampl.var["S"].to_dict(),
# "Q": ampl.var["Q"].to_dict(),
# }
UnitAssignment = pd.DataFrame({j: [None for t in TIME] for j in UNITS}, index=TIME)
for t in TIME:
for j in UNITS:
for i in I[j]:
for s in S_[i]:
if t - p[i] >= 0:
if solution["W"][i, j, max(TIME[TIME <= t - p[i]])] > 0:
UnitAssignment.loc[t, j] = None
for i in I[j]:
if solution["W"][i, j, t] > 0:
UnitAssignment.loc[t, j] = (i, solution["B"][i, j, t])
UnitAssignment
| Heater | Reactor_1 | Reactor_2 | Still | |
|---|---|---|---|---|
| 0 | None | (Reaction_1, 80) | (Reaction_1, 80) | None |
| 1 | (Heating, 95.99999999999866) | None | None | None |
| 2 | None | (Reaction_2, 80) | (Reaction_2, 80) | None |
| 3 | None | None | None | None |
| 4 | None | (Reaction_2, 79.99999999999514) | (Reaction_2, 5.275779813018744e-13) | None |
| 5 | (Heating, 17.33333333332865) | (Reaction_1, 6.9505290412053e-12) | (Reaction_1, 80) | (Separation, 5.115907697472721e-12) |
| 6 | None | (Reaction_2, 1.667406953250368e-12) | None | None |
| 7 | (Heating, 99.99999999999993) | (Reaction_3, 6.954437026251981e-12) | (Reaction_3, 80) | None |
| 8 | None | (Reaction_2, 79.99999999999842) | (Reaction_2, 79.99999999999991) | (Separation, 160.0000000000086) |
| 9 | None | (Reaction_1, 1.588229547877518e-12) | (Reaction_1, 7.958078640513123e-14) | None |
| 10 | None | (Reaction_3, 79.99999999999842) | (Reaction_3, 80) | None |
| 11 | None | (Reaction_2, 80) | (Reaction_2, 53.33333333333329) | (Separation, 160) |
| 12 | None | None | None | None |
| 13 | None | (Reaction_3, 80) | (Reaction_3, 39.99999999999996) | None |
| 14 | None | None | None | (Separation, 120) |
| 15 | None | None | None | None |
| 16 | None | None | None | None |
State inventories#
pd.DataFrame(
[[solution["S"][s, t] for s in STATES.keys()] for t in TIME],
columns=STATES.keys(),
index=TIME,
)
| Feed_B | Int_BC | Hot_A | Impure_E | Product_1 | Product_2 | Feed_A | Int_AB | Feed_C | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 420.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 0.000000 | 0.000000e+00 | 500.000000 | 0.0 | 420.0 |
| 1 | 420.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 0.000000 | 0.000000e+00 | 404.000000 | 0.0 | 420.0 |
| 2 | 420.0 | 64.0 | 3.200000e+01 | 0.000000e+00 | 0.000000 | 0.000000e+00 | 404.000000 | 0.0 | 420.0 |
| 3 | 420.0 | 64.0 | 3.200000e+01 | 0.000000e+00 | 0.000000 | 0.000000e+00 | 404.000000 | 0.0 | 420.0 |
| 4 | 420.0 | 16.0 | 3.929301e-13 | 0.000000e+00 | 64.000000 | 0.000000e+00 | 404.000000 | 32.0 | 404.0 |
| 5 | 380.0 | 16.0 | 0.000000e+00 | 8.000000e+01 | 64.000000 | 0.000000e+00 | 386.666667 | 32.0 | 364.0 |
| 6 | 340.0 | 16.0 | 1.733333e+01 | 8.000000e+01 | 96.000000 | 4.604317e-12 | 386.666667 | 80.0 | 324.0 |
| 7 | 340.0 | 96.0 | 1.733333e+01 | 8.000000e+01 | 96.000000 | 4.604317e-12 | 286.666667 | 16.0 | 308.0 |
| 8 | 340.0 | 80.0 | 5.333333e+01 | 0.000000e+00 | 96.000000 | 4.604317e-12 | 286.666667 | 16.0 | 308.0 |
| 9 | 340.0 | 80.0 | 5.333333e+01 | 1.582900e-12 | 96.000000 | 1.440000e+02 | 286.666667 | 16.0 | 308.0 |
| 10 | 340.0 | 80.0 | 5.333333e+01 | 1.582900e-12 | 160.000000 | 1.440000e+02 | 286.666667 | 0.0 | 276.0 |
| 11 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 160.000000 | 1.440000e+02 | 286.666667 | 0.0 | 276.0 |
| 12 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 160.000000 | 2.880000e+02 | 286.666667 | 0.0 | 276.0 |
| 13 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 213.333333 | 2.880000e+02 | 286.666667 | 0.0 | 252.0 |
| 14 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 213.333333 | 2.880000e+02 | 286.666667 | 0.0 | 252.0 |
| 15 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 213.333333 | 3.960000e+02 | 286.666667 | 0.0 | 252.0 |
| 16 | 340.0 | 0.0 | 0.000000e+00 | 0.000000e+00 | 213.333333 | 3.960000e+02 | 286.666667 | 12.0 | 252.0 |
from math import ceil
plt.figure(figsize=(10, 6))
for s, idx in zip(STATES.keys(), range(0, len(STATES.keys()))):
plt.subplot(ceil(len(STATES.keys()) / 3), 3, idx + 1)
tlast, ylast = 0, STATES[s]["initial"]
for t, y in zip(list(TIME), [solution["S"][s, t] for t in TIME]):
plt.plot([tlast, t, t], [ylast, ylast, y], "b")
# plt.plot([tlast,t],[ylast,y],'b.',ms=10)
tlast, ylast = t, y
plt.ylim(0, 1.1 * C[s])
plt.plot([0, H], [C[s], C[s]], "r--")
plt.title(s)
plt.tight_layout()

Unit batch inventories#
pd.DataFrame(
[[solution["Q"][j, t] for j in UNITS] for t in TIME], columns=UNITS, index=TIME
)
| Heater | Reactor_1 | Reactor_2 | Still | |
|---|---|---|---|---|
| 0 | 0.000000e+00 | 80.0 | 80.000000 | 0.000000e+00 |
| 1 | 9.600000e+01 | 80.0 | 80.000000 | 0.000000e+00 |
| 2 | 0.000000e+00 | 80.0 | 80.000000 | 0.000000e+00 |
| 3 | 0.000000e+00 | 80.0 | 80.000000 | 0.000000e+00 |
| 4 | 0.000000e+00 | 80.0 | 80.000000 | 0.000000e+00 |
| 5 | 1.733333e+01 | 80.0 | 80.000000 | 5.115908e-12 |
| 6 | -2.886580e-14 | 80.0 | 80.000000 | 5.115908e-13 |
| 7 | 1.000000e+02 | 80.0 | 80.000000 | 0.000000e+00 |
| 8 | 0.000000e+00 | 80.0 | 80.000000 | 1.600000e+02 |
| 9 | 0.000000e+00 | 80.0 | 80.000000 | 1.600000e+01 |
| 10 | 0.000000e+00 | 80.0 | 80.000000 | 0.000000e+00 |
| 11 | 0.000000e+00 | 80.0 | 53.333333 | 1.600000e+02 |
| 12 | 0.000000e+00 | 80.0 | 53.333333 | 1.600000e+01 |
| 13 | 0.000000e+00 | 80.0 | 40.000000 | 0.000000e+00 |
| 14 | 0.000000e+00 | 0.0 | 0.000000 | 1.200000e+02 |
| 15 | 0.000000e+00 | 0.0 | 0.000000 | 1.200000e+01 |
| 16 | 0.000000e+00 | 0.0 | 0.000000 | 0.000000e+00 |
Gannt chart#
plt.figure(figsize=(12, 6))
gap = H / 500
idx = 1
lbls = []
ticks = []
for j in sorted(UNITS):
idx -= 1
for i in sorted(I[j]):
idx -= 1
ticks.append(idx)
lbls.append("{0:s} -> {1:s}".format(j, i))
plt.plot([0, H], [idx, idx], lw=20, alpha=0.3, color="y")
for t in TIME:
if solution["W"][i, j, t] > 0:
plt.plot(
[t + gap, t + p[i] - gap],
[idx, idx],
"b",
lw=20,
solid_capstyle="butt",
)
txt = "{0:.2f}".format(solution["B"][i, j, t])
plt.text(
t + p[i] / 2,
idx,
txt,
color="white",
weight="bold",
ha="center",
va="center",
)
plt.xlim(0, H)
plt.gca().set_yticks(ticks)
plt.gca().set_yticklabels(lbls)

Trace of events and states#
sep = "\n--------------------------------------------------------------------------------------------\n"
print(sep)
print("Starting Conditions")
print(" Initial Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s, STATES[s]["initial"]))
units = {j: {"assignment": "None", "t": 0} for j in UNITS}
for t in TIME:
print(sep)
print("Time =", t, "hr")
print(" Instructions:")
for j in UNITS:
units[j]["t"] += 1
# transfer from unit to states
for i in I[j]:
for s in S_[i]:
if t - P[(i, s)] >= 0:
amt = (
rho_[(i, s)]
* solution["B"][i, j, max(TIME[TIME <= t - P[(i, s)]])]
)
if amt > 0:
print(" Transfer", amt, "kg from", j, "to", s)
for j in UNITS:
# release units from tasks
for i in I[j]:
if t - p[i] >= 0:
if solution["W"][i, j, max(TIME[TIME <= t - p[i]])] > 0:
print(" Release", j, "from", i)
units[j]["assignment"] = "None"
units[j]["t"] = 0
# assign units to tasks
for i in I[j]:
if solution["W"][i, j, t] > 0:
print(
" Assign",
j,
"with capacity",
Bmax[(i, j)],
"kg to task",
i,
"for",
p[i],
"hours",
)
units[j]["assignment"] = i
units[j]["t"] = 1
# transfer from states to starting tasks
for i in I[j]:
for s in S[i]:
amt = rho[(i, s)] * solution["B"][i, j, t]
if amt > 0:
print(" Transfer", amt, "kg from", s, "to", j)
print("\n Inventories are now:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s, solution["S"][s, t]))
print("\n Unit Assignments are now:")
for j in UNITS:
if units[j]["assignment"] != "None":
fmt = " {0:s} performs the {1:s} task with a {2:.2f} kg batch for hour {3:f} of {4:f}"
i = units[j]["assignment"]
print(fmt.format(j, i, solution["Q"][j, t], units[j]["t"], p[i]))
print(sep)
print("Final Conditions")
print(" Final Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s, solution["S"][s, H]))
--------------------------------------------------------------------------------------------
Starting Conditions
Initial Inventories:
Feed_B 500.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Feed_A 500.0 kg
Int_AB 0.0 kg
Feed_C 500.0 kg
--------------------------------------------------------------------------------------------
Time = 0 hr
Instructions:
Assign Reactor_1 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 40.0 kg from Feed_B to Reactor_1
Transfer 40.0 kg from Feed_C to Reactor_1
Assign Reactor_2 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 40.0 kg from Feed_B to Reactor_2
Transfer 40.0 kg from Feed_C to Reactor_2
Inventories are now:
Feed_B 420.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Feed_A 500.0 kg
Int_AB 0.0 kg
Feed_C 420.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 1 hr
Instructions:
Assign Heater with capacity 100 kg to task Heating for 1 hours
Transfer 95.99999999999866 kg from Feed_A to Heater
Inventories are now:
Feed_B 420.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Feed_A 404.0 kg
Int_AB 0.0 kg
Feed_C 420.0 kg
Unit Assignments are now:
Heater performs the Heating task with a 96.00 kg batch for hour 1.000000 of 1.000000
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 2 hr
Instructions:
Transfer 95.99999999999866 kg from Heater to Hot_A
Transfer 80.0 kg from Reactor_1 to Int_BC
Transfer 80.0 kg from Reactor_2 to Int_BC
Release Heater from Heating
Release Reactor_1 from Reaction_1
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_1
Transfer 32.0 kg from Hot_A to Reactor_1
Release Reactor_2 from Reaction_1
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_2
Transfer 32.0 kg from Hot_A to Reactor_2
Inventories are now:
Feed_B 420.0 kg
Int_BC 64.0 kg
Hot_A 32.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Feed_A 404.0 kg
Int_AB 0.0 kg
Feed_C 420.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 3 hr
Instructions:
Inventories are now:
Feed_B 420.0 kg
Int_BC 64.0 kg
Hot_A 32.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Feed_A 404.0 kg
Int_AB 0.0 kg
Feed_C 420.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 4 hr
Instructions:
Transfer 32.0 kg from Reactor_1 to Product_1
Transfer 48.0 kg from Reactor_1 to Int_AB
Transfer 32.0 kg from Reactor_2 to Product_1
Transfer 48.0 kg from Reactor_2 to Int_AB
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 5.5604232329642404e-12 kg from Int_AB to Reactor_1
Transfer 1.3901058082410601e-12 kg from Feed_C to Reactor_1
Transfer 47.99999999999708 kg from Int_BC to Reactor_1
Transfer 31.999999999998057 kg from Hot_A to Reactor_1
Release Reactor_2 from Reaction_2
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 63.9999999999999 kg from Int_AB to Reactor_2
Transfer 15.999999999999975 kg from Feed_C to Reactor_2
Transfer 3.165467887811246e-13 kg from Int_BC to Reactor_2
Transfer 2.1103119252074978e-13 kg from Hot_A to Reactor_2
Inventories are now:
Feed_B 420.0 kg
Int_BC 16.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 64.0 kg
Product_2 0.0 kg
Feed_A 404.0 kg
Int_AB 32.0 kg
Feed_C 404.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 5 hr
Instructions:
Transfer 6.9505290412053e-12 kg from Reactor_1 to Impure_E
Transfer 79.99999999999987 kg from Reactor_2 to Impure_E
Assign Heater with capacity 100 kg to task Heating for 1 hours
Transfer 17.33333333332865 kg from Feed_A to Heater
Release Reactor_1 from Reaction_3
Assign Reactor_1 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 3.47526452060265e-12 kg from Feed_B to Reactor_1
Transfer 3.47526452060265e-12 kg from Feed_C to Reactor_1
Release Reactor_2 from Reaction_3
Assign Reactor_2 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 40.0 kg from Feed_B to Reactor_2
Transfer 40.0 kg from Feed_C to Reactor_2
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 5.115907697472721e-12 kg from Impure_E to Still
Inventories are now:
Feed_B 380.0 kg
Int_BC 16.0 kg
Hot_A 0.0 kg
Impure_E 80.0 kg
Product_1 64.0 kg
Product_2 0.0 kg
Feed_A 386.7 kg
Int_AB 32.0 kg
Feed_C 364.0 kg
Unit Assignments are now:
Heater performs the Heating task with a 17.33 kg batch for hour 1.000000 of 1.000000
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 0.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 6 hr
Instructions:
Transfer 17.33333333332865 kg from Heater to Hot_A
Transfer 31.999999999998057 kg from Reactor_1 to Product_1
Transfer 47.99999999999708 kg from Reactor_1 to Int_AB
Transfer 2.1103119252074978e-13 kg from Reactor_2 to Product_1
Transfer 3.165467887811246e-13 kg from Reactor_2 to Int_AB
Transfer 4.604316927725449e-12 kg from Still to Product_2
Release Heater from Heating
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_1 for 2 hours
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 39.99999999999569 kg from Feed_B to Reactor_1
Transfer 39.99999999999569 kg from Feed_C to Reactor_1
Transfer 1.0004441719502207e-12 kg from Int_BC to Reactor_1
Transfer 6.669627813001472e-13 kg from Hot_A to Reactor_1
Release Reactor_2 from Reaction_2
Inventories are now:
Feed_B 340.0 kg
Int_BC 16.0 kg
Hot_A 17.3 kg
Impure_E 80.0 kg
Product_1 96.0 kg
Product_2 0.0 kg
Feed_A 386.7 kg
Int_AB 80.0 kg
Feed_C 324.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 0.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 7 hr
Instructions:
Transfer 6.9505290412053e-12 kg from Reactor_1 to Int_BC
Transfer 80.0 kg from Reactor_2 to Int_BC
Transfer 5.115907697472721e-13 kg from Still to Int_AB
Assign Heater with capacity 100 kg to task Heating for 1 hours
Transfer 99.99999999999993 kg from Feed_A to Heater
Release Reactor_1 from Reaction_1
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 5.563549621001585e-12 kg from Int_AB to Reactor_1
Transfer 1.3908874052503963e-12 kg from Feed_C to Reactor_1
Release Reactor_2 from Reaction_1
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 64.0 kg from Int_AB to Reactor_2
Transfer 16.0 kg from Feed_C to Reactor_2
Release Still from Separation
Inventories are now:
Feed_B 340.0 kg
Int_BC 96.0 kg
Hot_A 17.3 kg
Impure_E 80.0 kg
Product_1 96.0 kg
Product_2 0.0 kg
Feed_A 286.7 kg
Int_AB 16.0 kg
Feed_C 308.0 kg
Unit Assignments are now:
Heater performs the Heating task with a 100.00 kg batch for hour 1.000000 of 1.000000
Reactor_1 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
Reactor_2 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 8 hr
Instructions:
Transfer 99.99999999999993 kg from Heater to Hot_A
Transfer 79.99999999999137 kg from Reactor_1 to Int_BC
Transfer 6.954437026251981e-12 kg from Reactor_1 to Impure_E
Transfer 6.669627813001472e-13 kg from Reactor_1 to Product_1
Transfer 1.0004441719502207e-12 kg from Reactor_1 to Int_AB
Transfer 80.0 kg from Reactor_2 to Impure_E
Release Heater from Heating
Release Reactor_1 from Reaction_1
Release Reactor_1 from Reaction_3
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 1.2663203818874536e-12 kg from Int_AB to Reactor_1
Transfer 3.165800954718634e-13 kg from Feed_C to Reactor_1
Transfer 47.999999999999055 kg from Int_BC to Reactor_1
Transfer 31.99999999999937 kg from Hot_A to Reactor_1
Release Reactor_2 from Reaction_3
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 47.99999999999995 kg from Int_BC to Reactor_2
Transfer 31.999999999999968 kg from Hot_A to Reactor_2
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 160.0000000000086 kg from Impure_E to Still
Inventories are now:
Feed_B 340.0 kg
Int_BC 80.0 kg
Hot_A 53.3 kg
Impure_E 0.0 kg
Product_1 96.0 kg
Product_2 0.0 kg
Feed_A 286.7 kg
Int_AB 16.0 kg
Feed_C 308.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 160.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 9 hr
Instructions:
Transfer 1.582900477359317e-12 kg from Reactor_1 to Impure_E
Transfer 144.00000000000776 kg from Still to Product_2
Release Reactor_1 from Reaction_3
Assign Reactor_1 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 7.94114773938759e-13 kg from Feed_B to Reactor_1
Transfer 7.94114773938759e-13 kg from Feed_C to Reactor_1
Assign Reactor_2 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 3.9790393202565614e-14 kg from Feed_B to Reactor_2
Transfer 3.9790393202565614e-14 kg from Feed_C to Reactor_2
Inventories are now:
Feed_B 340.0 kg
Int_BC 80.0 kg
Hot_A 53.3 kg
Impure_E 0.0 kg
Product_1 96.0 kg
Product_2 144.0 kg
Feed_A 286.7 kg
Int_AB 16.0 kg
Feed_C 308.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 16.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 10 hr
Instructions:
Transfer 31.99999999999937 kg from Reactor_1 to Product_1
Transfer 47.999999999999055 kg from Reactor_1 to Int_AB
Transfer 31.999999999999968 kg from Reactor_2 to Product_1
Transfer 47.99999999999995 kg from Reactor_2 to Int_AB
Transfer 16.000000000000863 kg from Still to Int_AB
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 63.99999999999874 kg from Int_AB to Reactor_1
Transfer 15.999999999999686 kg from Feed_C to Reactor_1
Release Reactor_2 from Reaction_2
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 64.0 kg from Int_AB to Reactor_2
Transfer 16.0 kg from Feed_C to Reactor_2
Release Still from Separation
Inventories are now:
Feed_B 340.0 kg
Int_BC 80.0 kg
Hot_A 53.3 kg
Impure_E 0.0 kg
Product_1 160.0 kg
Product_2 144.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 276.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
Reactor_2 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 11 hr
Instructions:
Transfer 1.588229547877518e-12 kg from Reactor_1 to Int_BC
Transfer 79.99999999999842 kg from Reactor_1 to Impure_E
Transfer 7.958078640513123e-14 kg from Reactor_2 to Int_BC
Transfer 80.0 kg from Reactor_2 to Impure_E
Release Reactor_1 from Reaction_1
Release Reactor_1 from Reaction_3
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_1
Transfer 32.0 kg from Hot_A to Reactor_1
Release Reactor_2 from Reaction_1
Release Reactor_2 from Reaction_3
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 31.999999999999975 kg from Int_BC to Reactor_2
Transfer 21.333333333333318 kg from Hot_A to Reactor_2
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 160.0 kg from Impure_E to Still
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 160.0 kg
Product_2 144.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 276.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 53.33 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 160.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 12 hr
Instructions:
Transfer 144.0 kg from Still to Product_2
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 160.0 kg
Product_2 288.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 276.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Reactor_2 performs the Reaction_2 task with a 53.33 kg batch for hour 2.000000 of 2.000000
Still performs the Separation task with a 16.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 13 hr
Instructions:
Transfer 32.0 kg from Reactor_1 to Product_1
Transfer 48.0 kg from Reactor_1 to Int_AB
Transfer 21.333333333333318 kg from Reactor_2 to Product_1
Transfer 31.999999999999975 kg from Reactor_2 to Int_AB
Transfer 16.0 kg from Still to Int_AB
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 64.0 kg from Int_AB to Reactor_1
Transfer 16.0 kg from Feed_C to Reactor_1
Release Reactor_2 from Reaction_2
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 31.999999999999968 kg from Int_AB to Reactor_2
Transfer 7.999999999999992 kg from Feed_C to Reactor_2
Release Still from Separation
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 213.3 kg
Product_2 288.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 252.0 kg
Unit Assignments are now:
Reactor_1 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
Reactor_2 performs the Reaction_3 task with a 40.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 14 hr
Instructions:
Transfer 80.0 kg from Reactor_1 to Impure_E
Transfer 39.99999999999996 kg from Reactor_2 to Impure_E
Release Reactor_1 from Reaction_3
Release Reactor_2 from Reaction_3
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 120.0 kg from Impure_E to Still
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 213.3 kg
Product_2 288.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 252.0 kg
Unit Assignments are now:
Still performs the Separation task with a 120.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 15 hr
Instructions:
Transfer 108.0 kg from Still to Product_2
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 213.3 kg
Product_2 396.0 kg
Feed_A 286.7 kg
Int_AB 0.0 kg
Feed_C 252.0 kg
Unit Assignments are now:
Still performs the Separation task with a 12.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 16 hr
Instructions:
Transfer 12.0 kg from Still to Int_AB
Release Still from Separation
Inventories are now:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 213.3 kg
Product_2 396.0 kg
Feed_A 286.7 kg
Int_AB 12.0 kg
Feed_C 252.0 kg
Unit Assignments are now:
--------------------------------------------------------------------------------------------
Final Conditions
Final Inventories:
Feed_B 340.0 kg
Int_BC 0.0 kg
Hot_A 0.0 kg
Impure_E 0.0 kg
Product_1 213.3 kg
Product_2 396.0 kg
Feed_A 286.7 kg
Int_AB 12.0 kg
Feed_C 252.0 kg





